Hvordan til at beregne afstanden til horisonten

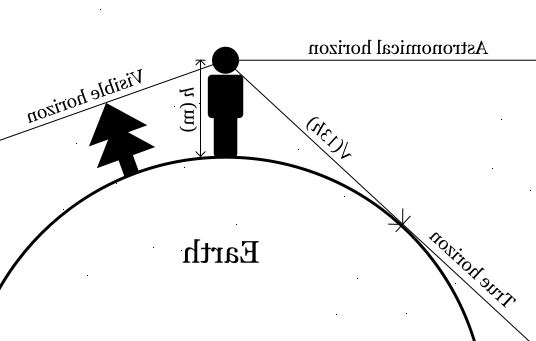
1. 1
   Mål din "øjenhøjde". Mål længden mellem jorden og dine i meter eller fod. En måde at beregne dette er at måle afstanden mellem din og toppen af dit hoved. Fratræk denne værdi fra din totalhøjde, og hvad der vil blive efterladt er afstanden mellem dine øjne og overfladen du står på. Hvis du står præcis ved havoverfladen, med bunden af ​​dine fødder i niveau med vandet, er dette den eneste måling, du behøver.
2. 2
   Tilføj din "lokale elevation", hvis du står på en hævet overflade, såsom en bakke, bygning eller båd. Hvor mange meter eller fod over den sande horisont står du? 1 meter? 4.000 fødder? Det tilføjes, at nummeret til dit øjenhøjde (i samme enheder, naturligvis).
3. 3
   Multiplicer med 13m hvis du tog måling i meter, eller gang med 1.5ft hvis du tog måling i fødderne.
4. 4
   Tag kvadratroden for at finde svaret. Hvis du har brugt meter, vil dit svar være i kilometer, og hvis fødder, vil svaret være i miles. Den beregnede afstanden er en lige linje fra dine øjne til horisonten. Den faktiske afstand, du vil rejse for at komme til horisonten bliver længere på grund af overfladen krumning og (på land) uregelmæssigheder. Fortsæt til næste metode nedenfor for en mere nøjagtig (og kompliceret) formel.
5. 5
   Forstå, hvordan denne beregning virker. Det er baseret på en trekant dannet af din observation point (øjnene), den sande horisont point (hvad du ser på) og centrum af Jorden. Ved at kende radius af Jorden og måle din øjenhøjde og lokale elevation, efterlader det kun er afstanden mellem dine øjne og horisonten som ukendt. Da sider af trekanten, der mødes ved horisonten faktisk danner en ret vinkel, kan vi bruge Pythagoras læresætning (gode gamle a ^ 2 + b ^ 2 = c ^ 2), som grundlag for denne beregning, hvor:
   • a = R (radius af Jorden)
   • b = afstanden til horisonten, ukendte
   • c = h (din øjenhøjde) + R

Alternativ metode # 1

1. 1
   Beregne den faktiske afstand, du er nødt til at krydse for at komme til horisonten ved hjælp af denne formel:
   d = R * ARccOS (R / (R + h))
   d = afstand til horisonten
   h = højden af ​​øjet
   
2. 2
   Øge F med 20% for at kompensere for den forvridende brydning af lysstråler, og at nå frem til en mere nøjagtig måling. Den geometriske horisont beregnes efter metoden i denne artikel, kan ikke være den samme som den optiske horisont, hvilket er, hvad dit øje faktisk ser. Atmosfæren bøjninger (refracts) lys, der er på rejse horisontalt. Hvad det betyder normalt, at en stråle af lys er i stand til let følge af jordens krumning, så den optiske horisont er en smule længere væk end den geometriske horisont. Desværre brydning på grund af atmosfæren er hverken konstant eller forudsigelig, da det afhænger af ændringen af ​​temperaturen med højden. Der er derfor ingen enkel måde at tilføje en rettelse til formlen for den geometriske horisont, selv om man kan opnå en "gennemsnitlige" korrektion ved at antage en radius for jorden, der er en smule større end den sande radius.
3. 3
   Finde ud af, hvordan denne beregning virker. Dette vil beregne længden af ​​den buede linje, der følger fra fødderne til den sande horisont (vist med grønt på dette billede). Nu ARccOS (R / (R + h)) portion refererer til den vinkel, der er lavet i midten af ​​jorden ved linje går fra den sande horisont til centrum og linje går fra dig til centrum. Med denne vinkel, multiplicere vi det ved R for at få "lysbuelængde", som i dette tilfælde, er den afstand, du er på udkig efter.
   

Alternativ metode # 2

1. 1
   Antag en flad fly eller havet. Denne metode er en forenklet version af den første sæt af instruktioner præsenteret i denne artikel, og gælder kun i fod og miles.
2. 2
   Løs for afstanden i miles ved at tilslutte din øjenhøjde i fod (h) i følgende formel:
   d = 1,2246 * sqrt (h)
   
3. 3
   Udled formlen fra Pythagoras 'læresætning.
   (R + h) ^ 2 = R ^ 2 + d ^ 2
   Løsning for h (. Gøre den antagelse, at R->> h og udtrykker radius af jorden i miles, ca 3959) giver udtryk:
   d = sqrt (2 * R * h)